HSV Color model (RGB to HSV)

HSV  cylinder

Range of Hue : [0 - 2π)

Range of Saturation : [0 - 1)

Range of Value : [0 - 255)

Hue and chroma

Fig. 9. Both hue and chroma are defined based on the projection of the RGB cube onto a hexagon in the "chromaticity plane". Chroma is the relative size of the hexagon passing through a point, and hue is how far around that hexagon’s edge the point lies.

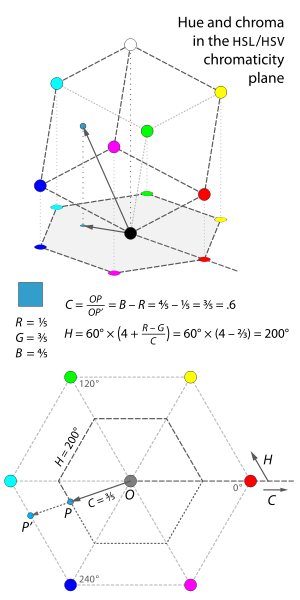
In each of our models, we calculate both hue and what this article will call chroma, after Joblove and Greenberg, in the same way—that is, the hue of a color has the same numerical values in all of these models, as does its chroma. If we take our tilted RGB cube, and project it onto the "chromaticityplane" perpendicular to the neutral axis, our projection takes the shape of a hexagon, with red, yellow, green, cyan, blue, and magenta at its corners (fig. 9). 

(RGB color model 큐브를 정사영시키면 6가지 색상을 갖는 hexagon 형태를 얻을 수 있다.)

Hue is roughly the angle of thevector to a point in the projection, with red at 0°, while chroma is roughly the distance of the point from the origin.

More precisely, both hue and chroma in this model are defined with respect to the hexagonal shape of the projection. The chroma is the proportion of the distance from the origin to the edge of the hexagon. In the lower part of the diagram to the right, this is the ratio of lengths OP/OP′, or alternately the ratio of the radii of the two hexagons. This ratio is the difference between the largest and smallest values among R, G, or B in a color. To make our definitions easier to write, we’ll define these maximum and minimum component values as M and m, respectively

${\displaystyle {\begin{aligned}M&=\operatorname {max} (R,G,B)\\m&=\operatorname {min} (R,G,B)\\C&=M-m\end{aligned}}}$

To understand why chroma can be written as M − m, notice that any neutral color, with R = G = B, projects onto the origin and so has 0 chroma. Thus if we add or subtract the same amount from all three of R, G, and B, we move vertically within our tilted cube, and do not change the projection. Therefore, the two colors (R, G, B) and (R − m, G − m, B − m) project on the same point, and have the same chroma. The chroma of a color with one of its components equal to zero (m = 0) is simply the maximum of the other two components. This chroma is M in the particular case of a color with a zero component, and M − m in general.

The hue is the proportion of the distance around the edge of the hexagon which passes through the projected point, originally measured on the range [0, 1) but now typically measured in degrees[0°, 360°). For points which project onto the origin in the chromaticity plane (i.e., grays), hue is undefined. Mathematically, this definition of hue is written piecewise:^[20]

${\displaystyle {\begin{aligned}H^{\prime }&={\begin{cases}\mathrm {undefined} ,&{\mbox{if }}C=0\\{\frac {G-B}{C}}\;{\bmod {6}},&{\mbox{if }}M=R\\{\frac {B-R}{C}}+2,&{\mbox{if }}M=G\\{\frac {R-G}{C}}+4,&{\mbox{if }}M=B\end{cases}}\\H&=60^{\circ }\times H^{\prime }\end{aligned}}}$

Saturation

Fig. 14a–d. In both HSL and HSV, saturation is simply the chroma scaled to fill the interval [0, 1] for every combination of hue and lightness or value.

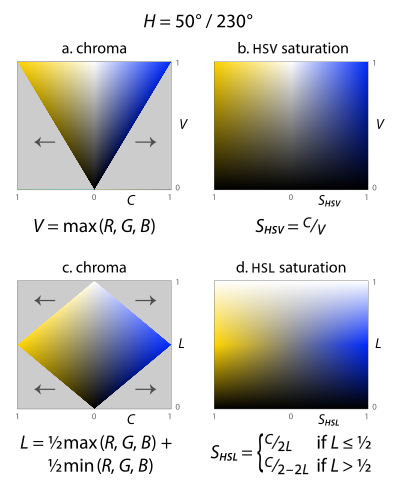
If we encode colors in a hue/lightness/chroma or hue/value/chroma model (using the definitions from the previous two sections), not all combinations of lightness (or value) and chroma are meaningful: that is, half of the colors we can describe usingH ∈ [0°, 360°), C ∈ [0, 1], andV ∈ [0, 1] fall outside the RGB gamut (the gray parts of the slices in figure 14). The creators of these models considered this a problem for some uses. For example, in a color selection interface with two of the dimensions in a rectangle and the third on a slider, half of that rectangle is made of unused space. Now imagine we have a slider for lightness: the user’s intent when adjusting this slider is potentially ambiguous: how should the software deal with out-of-gamut colors? Or conversely, If the user has selected as colorful as possible a dark purple  , and then shifts the lightness slider upward, what should be done: would the user prefer to see a lighter purple still as colorful as possible for the given hue and lightness  , or a lighter purple of exactly the same chroma as the original color  ?^[9]

To solve problems such as these, the HSL and HSV models scale the chroma so that it always fits into the range [0, 1] for every combination of hue and lightness or value, calling the new attributesaturation in both cases (fig. 14). To calculate either, simply divide the chroma by the maximum chroma for that value or lightness.

${\displaystyle {\begin{aligned}S_{HSV}&={\begin{cases}0,&{\mbox{if }}C=0\\{\frac {C}{V}},&{\mbox{otherwise}}\end{cases}}\\S_{HSL}&={\begin{cases}0,&{\mbox{if }}C=0\\{\frac {C}{1-|2L-1|}},&{\mbox{otherwise}}\end{cases}}\end{aligned}}}$

Reference : https://en.wikipedia.org/wiki/HSL_and_HSV